Rule110.exe 256 universi discreti

"Potrebbe forse essere che da qualche parte là fuori, nell'universo computazionale, troveremo il nostro universo fisico?"

Un automa cellulare consiste in una griglia regolare in un numero finito di dimensioni in cui ogni cella può essere in uno e uno solo di un numero finito di stati. L'evoluzione nel tempo è determinata da una regola che permette di passare da una configurazione data al tempo $t$ a quella successiva al tempo $t + 1$.

Siamo quindi di fronte a sistemi discreti in 3 sensi e modi distinti: lo spazio è discreto (a griglia), il tempo è discreto (si passa dal tempo $t$ al tempo $t + 1$) e il contenuto dello spaziotempo è discreto (si ha un numero finito di stati).

L'automa unidimensionale a due stati

Il più semplice automa cellulare non banale è unidimensionale (con meno di una dimensione ci si ritroverebbe con un'unica cella), con due soli possibili stati (con meno di due stati ci si ritroverebbe con un automa privo di contenuto) e in cui lo stato di una cella può dipendere solo dallo stato della cella stessa e dallo stato delle due celle adiacenti (i casi in cui si riduce ulteriormente la dipendenza rientrano in questo come sottoinsiemi particolari di regole).

È facile rendersi conto che per un siffatto automa abbiamo in tutto $256$ possibili regole, come si evince facilmente enumerando le possibili configurazioni di $3$ celle, che sono $2^3 = 8$, e considerando che per ognuna di esse si deve fornire uno tra $2$ possibili risultati, il che ci da in tutto proprio $2^8 = 256$ possibili regole.

Codifica delle regole

Ogni regola può quindi essere identificata da un numero binario di 8 cifre, quindi da un byte. Ad esempio la regola 110 (in decimale) sarà rappresentata dal byte 01101110, interpretando i bit nel seguente modo:

111 110 101 100 011 010 001 000
 0   1   1   0   1   1   1   0

dove la prima riga indica la configurazione delle 3 celle di partenza (adiacente a sinistra, centrale e adiacente a destra), mentre la seconda riga indica lo stato che dovrà prendere la cella centrale al ciclo successivo.

Visualizzazione e funzionalità

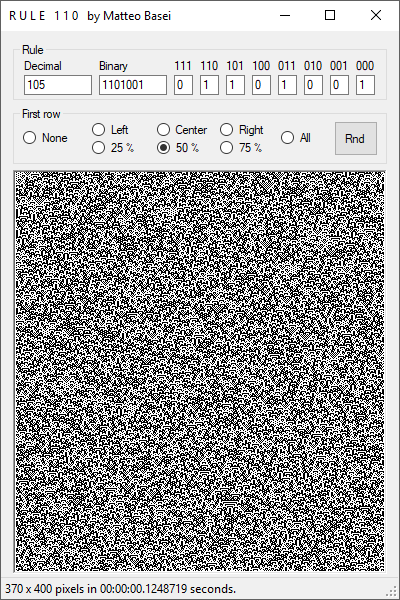
Studiando gli automi unidimensionale è molto comodo il fatto che occupando un'unica dimensione si può facilmente rappresentare la loro evoluzione nel tempo con un'immagine bidimensionale. In questa implementazione i vari cicli sono rappresentati da righe dall'alto al basso. È possibile scegliere la regola digitando il corrispondente numero in decimale, in binario, o indicando lo stato della cella al ciclo successivo caso per caso.

Oltre alla scelta della regola è possibile scegliere tra 8 diverse righe iniziali: completamente bianca, completamente nera, con un singolo punto nero a sinistra, a destra o in centro, e infine con il 25%, 50% o 75% di punti neri disposti in modo casuale. È presente anche un pulsante "random" che propone casualmente delle configurazioni tra un set predeterminato di configurazioni che generano un risultato particolarmente interessante.

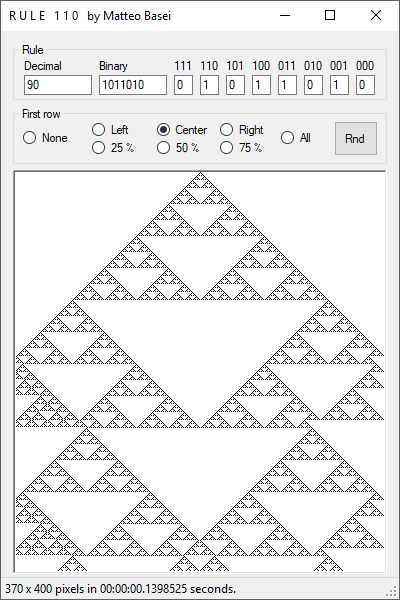
Una regola molto interessante è la regola 90 (01011010 in binario), che quando eseguita a partire da una riga completamente bianca con un singolo punto nero al centro, genera un triangolo di Sierpinski, un famoso frattale (a tal proposito vedi anche R-Paint).

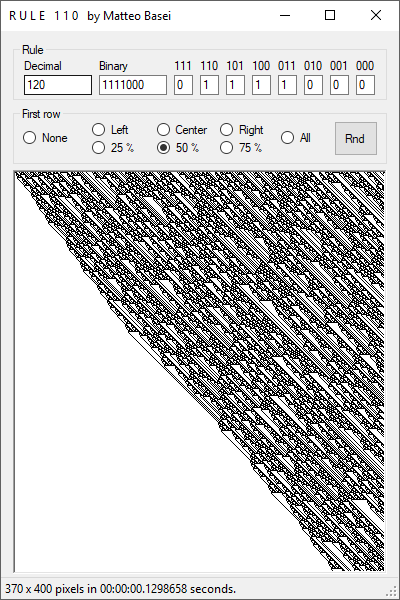
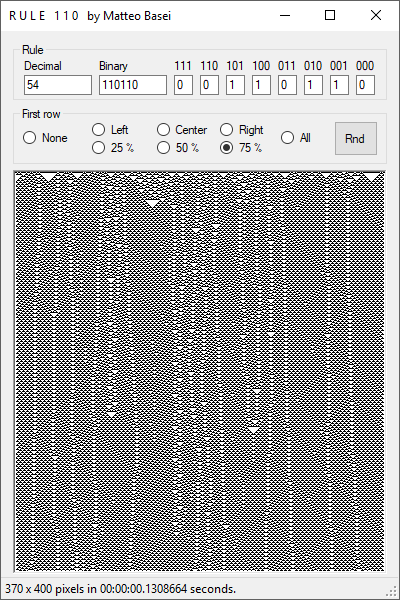
Il nome del programma viene dal numero di un'altra regola molto interessante, la regola 110 (01101110 in binario), una delle più famose.

Gli automi cellulari e i comportamenti emergenti

Una delle cose interessanti di questa regola è che, come molti altri automi cellulari, presenta un comportamento emergente. Inoltre tale schema emergente è di tipo particellare (e se non l'avete notato, anche da queste parti ci sono comportamenti emergenti di tipo particellare...).

Questo comportamento emergente è particolarmente evidente partendo da una riga iniziale random:

e può essere ulteriormente evidenziato applicando un semplice filtro all'immagine risultante:

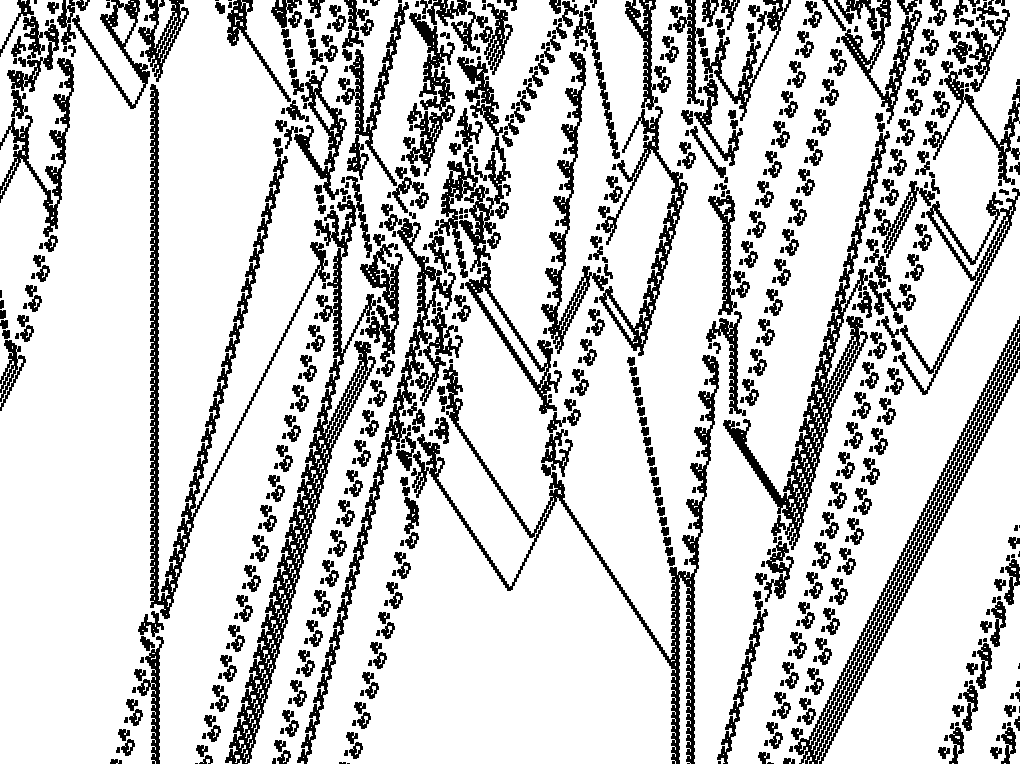
Questo esempio mostra come un comportamento apparentemente arbitrario e complesso, come un insieme di particelle di varia natura che si propagano nello spazio e interagiscono trasformandosi in particelle di natura differente quando collidono, possa in realtà emergere in modo molto naturale da uno schema di regole sottostante molto semplice e che a prima vista non ha nulla a che fare con la fenomenologia osservata.