Lissajous interferenze, battimenti e polarizzazione

"La carriera di un giovane fisico teorico consiste nel trattare l'oscillatore armonico a livelli di astrazione sempre crescenti."

Sidney Coleman

Questo semplice programma didattico permette di disegnare due sinusoidi arbitrarie $x(t)$ e $y(t)$, definendo per ognuna di esse le ampiezze $A_x$ e $A_y$, le pulsazioni $\omega_x = 2 \pi f_x$ e $\omega_y = 2 \pi f_y$ e le fasi iniziali $\theta_x$ e $\theta_y$ $$ \begin{alignedat}{2} x(t) &= A_x \cos \left( \omega_x t + \theta_x \right) \\[1ex] y(t) &= A_y \cos \left( \omega_y t + \theta_y \right) \end{alignedat} $$ È possibile osservare il modo in cui questi due segnali interferiscono nel segnale risultante $x(t) + y(t)$, generando varie figure, come ad esempio il fenomeno dei battimenti. Inoltre, interpretando $x(t)$ e $y(t)$ come componente orizzontale e verticale di un'onda trasversale, è possibile visualizzarne la polarizzazione, nel caso in cui le sinusoidi siano in fase, o le figure di Lissajous (che danno il nome al programma), nel caso in cui non lo siano.

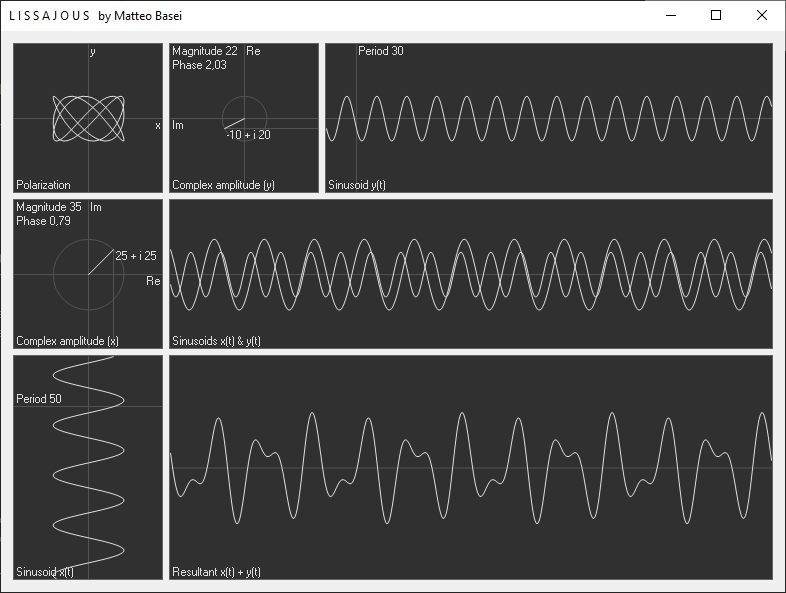
Interferenza e figura di Lissajous prodotte con due sinusoidi a differente frequenza. Come esempio della varietà di figure di intereferenza che si possono generare, in questo caso la sequenza segue lo schema del classico paradiddle RLRR LRLL (uno dei cosiddetti rudimenti dello studio delle percussioni).

Polarizzazione

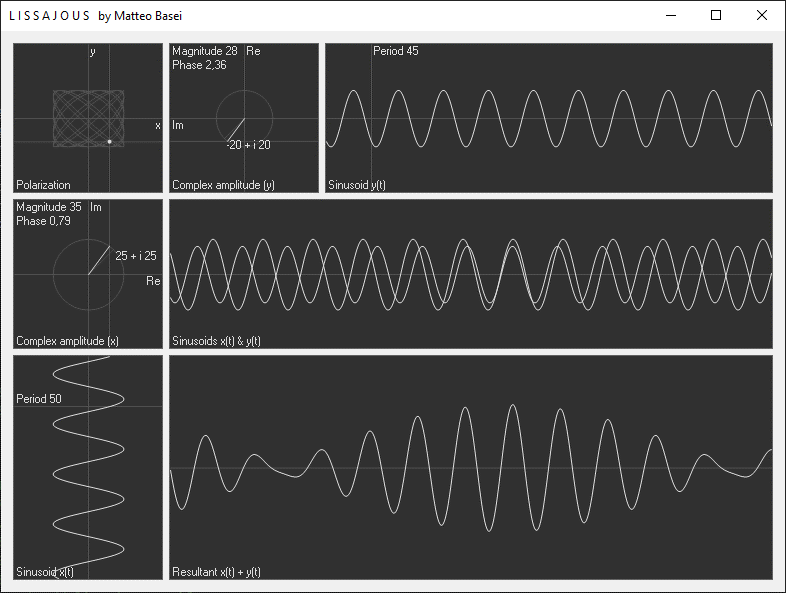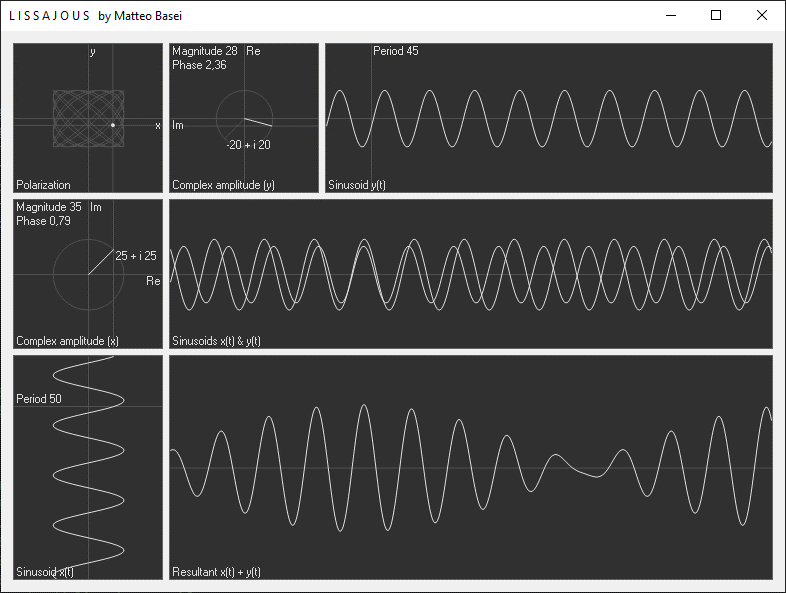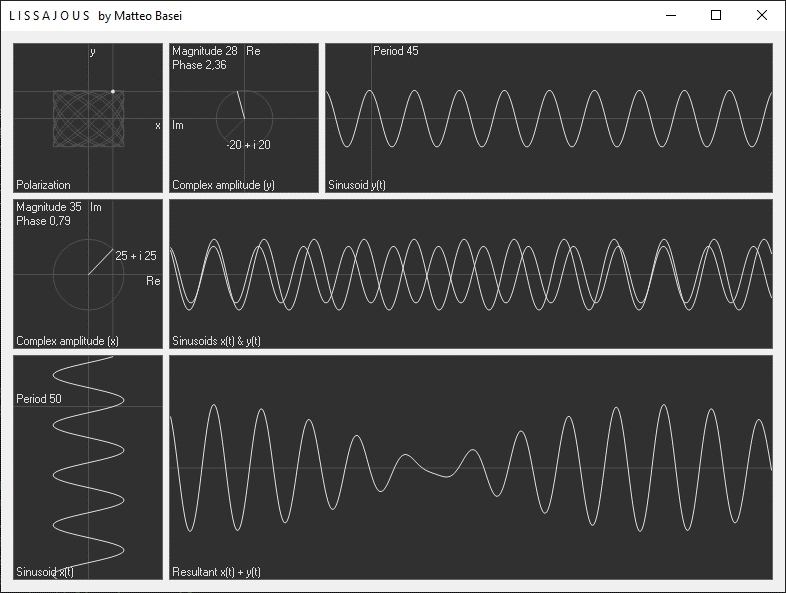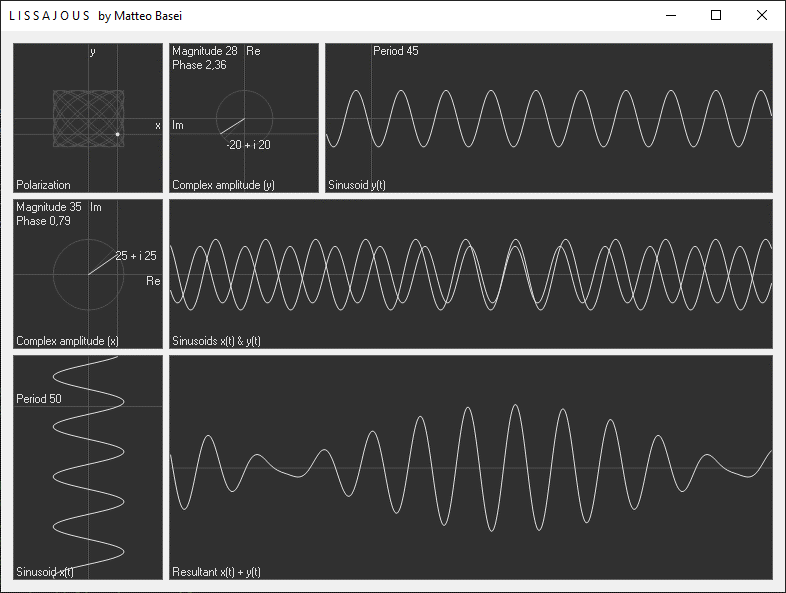
La finestra del programma è suddivisa in 7 riquadri. Il primo in alto a sinistra mostra la polarizzazione che si ottiene interpretando le due sinusoidi come componenti $x$ e $y$ di un'onda trasversale.

Un'onda trasversale è un'onda in cui le oscillazioni avvengono perpendicolarmente alla direzione di propagazione, quindi possono essere rappresentate da due numeri che corrispondono alle due direzioni mutuamente perpendicolari che sono a loro volta perpendicolari alla direzione di propagazione. Un classico esempio sono le onde elettromagnetiche, che sono onde puramente trasversali, cioè sono equivalenti alle vibrazioni che si propagherebbero in un mezzo ideale perfettamente rigido.

Al contrario le onde longitudinali sono le oscillazioni nella direzione di propagazione. Ad esempio le onde sonore, propagandosi in un mezzo, l'aria, che essendo un gas ha rigidità nulla, sono onde puramente longitudinali, quindi di compressione e decompressione nella direzione di propagazione e possono essere espresse da un singolo numero (la pressione sonora). Le onde sismiche, le vibrazioni della crosta terrestre, sono invece sia trasversali che longitudinali (quindi sono necessari tre numeri per rappresentarle);

Quando le due sinusoidi hanno la medesima frequenza ($\omega_x = \omega_y$) in questo riquadro si possono osservare i tre tipi di polarizzazione possibile: la polarizzazione lineare, circolare ed ellittica. La polarizzazione non è altro che l'immagine che viene creata (e visualizzata in questo riquadro) dall'oscillazione nelle due direzioni. Se le due sinusoidi sono in fase o sfasate di $\pi$ si ha polarizzazione lineare, nel riquadro compare un segmento e le ampiezze delle sinusoidi determinano l'inclinazione del segmento. Se le due sinusoidi sono sfasate di un angolo retto e le ampiezze sono le medesime si ha la polarizzazione circolare e si ottiene l'immagine di un cerchio. In tutti gli altri casi si ha la polarizzazione ellittica, che corrisponde al caso più generale, in quanto il segmento e il cerchio possono essere viste come ellissi degeneri.

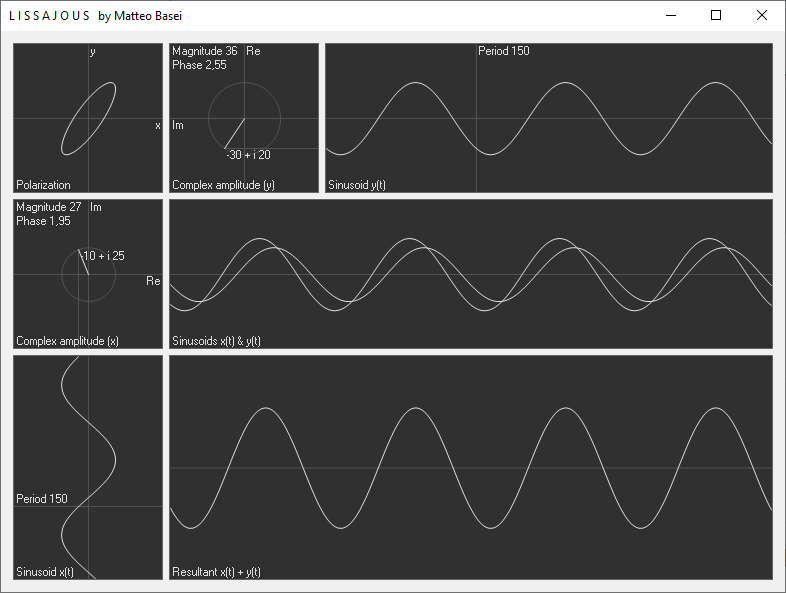
Polarizzazione ellittica generata da due sinusoidi alla medesima frequenza, ma con fase e ampiezze differenti. — Polarizzazione ellittica generata da due sinusoidi con medesima frequenza, ma fase e ampiezza differenti.

L'ampiezza complessa

Rispettivamente al di sotto e a destra del primo riquadro è possibile visualizzare e modificare (usando mouse o tastiera) l'ampiezza e la fase iniziale (quindi lo sfasamento relativo tra le due sinusoidi), espresse attraverso l'ampiezza complessa (se non ti è familiare la rappresentazione geometrica dei numeri complessi prima di continuare potresti dare un'occhiata alla pagina di un altro mio programma, Argand.exe).

Questa comoda rappresentazione è possibile in sostanza perché un'oscillazione lineare può essere vista come l'ombra di una rotazione. Infatti, utilizzando la formula di Eulero si ha $$ \begin{alignedat}{2} f(t) &= A \cos \left( \omega \, t + \theta \right) \\ &= \text{Re} \Big( A \big( \cos \left( \omega \, t + \theta \right) + i \, \sin \left( \omega \, t + \theta \right) \big) \Big) \\ &= \text{Re} \! \left( A \, e^{i \left( \omega \, t \, + \, \theta \right)} \right) \\ &= \text{Re} \! \left( A \, e^{i \, \omega \, t} e^{i \, \theta} \right) \\ &= \text{Re} \! \left( \xi \, e^{i \, \omega \, t} \right) \end{alignedat} $$ dove $\xi = A \, e^{i \, \theta}$ è appunto l'ampiezza complessa corrispondente all'ampiezza $A$ e alla fase $\theta$.

Le frequenze (e quindi le pulsazioni) vengono invece determinate indicando i periodi $T_x = 1 / f_x$ e $T_y = 1 / f_y$ delle sinusoidi.

Le figure di Lissajous

Sotto il riquadro con l'ampiezza complessa del segnale $y(t)$ e a destra di quello del segnale $x(t)$ ci sono i grafici delle due sinusoidi, con la possibilità, anche qui con mouse o tastiera, di modificarne la lunghezza d'onda, che corrisponde alla durata (in secondi, simbolo $\text{s}$) di un'oscillazione completa, e conseguentemente di modificarne quindi la frequenza, che è l'inverso della lunghezza d'onda, ovvero il numero di oscillazioni complete che si hanno nell'unità di tempo (in hertz, simbolo $\text{Hz}$).

Impostando due differenti periodi per le due sinusoidi è possibile osservare nel primo riquadro le cosiddette figure di Lissajous o di Bowditch, così chiamate in onore di Jules Antoine Lissajous e Nathaniel Bowditch che per primi e indipendentemente le studiarono nell'ottocento. Impostando invece il medesimo periodo e variando le due ampiezze complesse le figure di Lissajous scompaiono (o si riconducono a figure di Lissajous banali, a seconda di come si preferisce vederla) ed è possibile osservare la polarizzazione lineare, circolare ed ellittica.

Oltre alla linea, il cerchio e l'ellisse, che come abbiamo già detto possono essere osservate per $\omega_x = \omega_y$, si può osservare una parabola per determinati valori delle fase quando le frequenze sono una il doppio dell'altra.

Negli altri casi solo se $\omega_x / \omega_y$ è razionale le figure di Lissajous sono chiuse, e in questo caso ricordano dei nodi tridimensionali. Variando la fase di una delle due sinusoidi è anche possibile farli ruotare intorno all'asse corrispondente alla sinusoide con frequenza minore. In teoria dei nodi si chiamano nodi di Lissajous i nodi le cui proiezioni corrispondono alle figure di Lissajous di questo tipo.

In meccanica celeste le orbite di Lissajous sono orbite oscillanti intorno ai pundi di equilibrio lagrangiani collineari (vedi Lagrange).

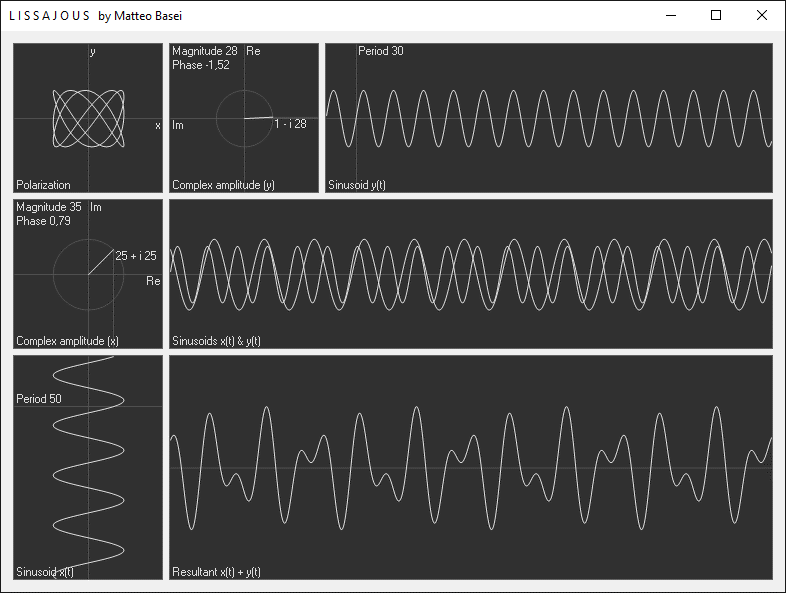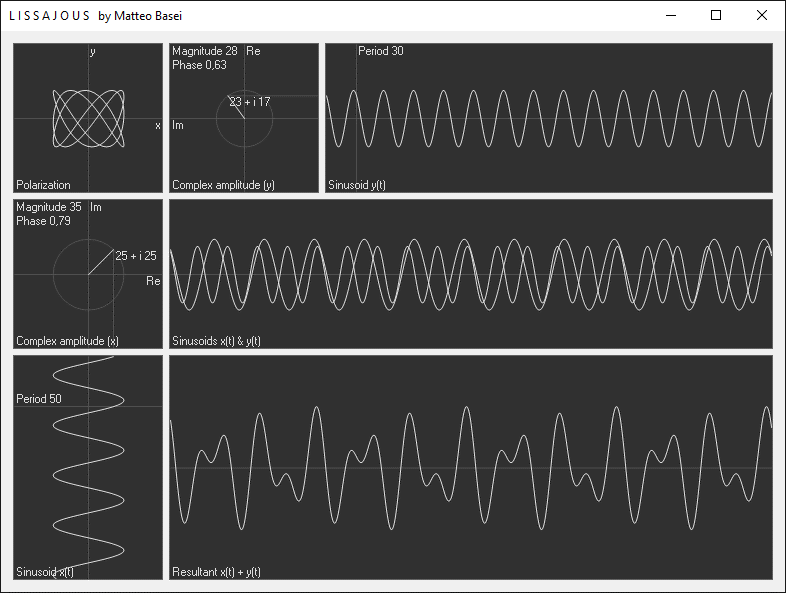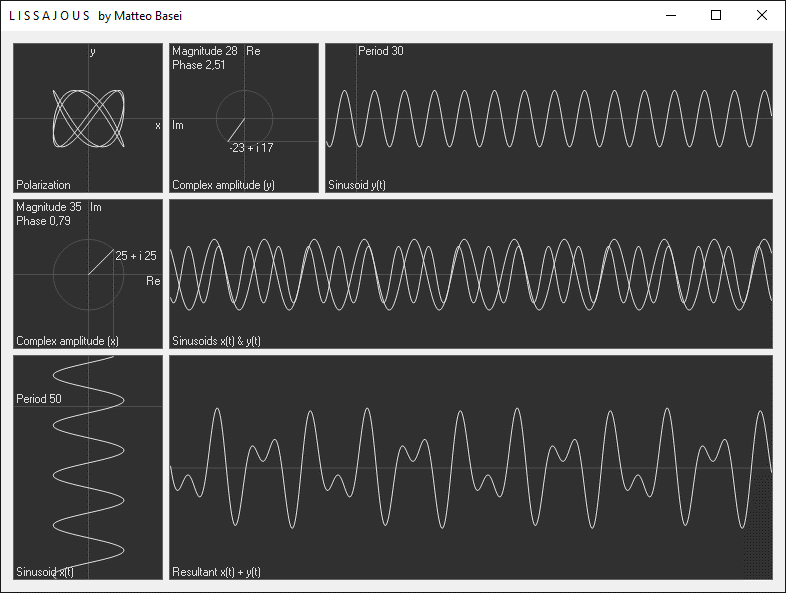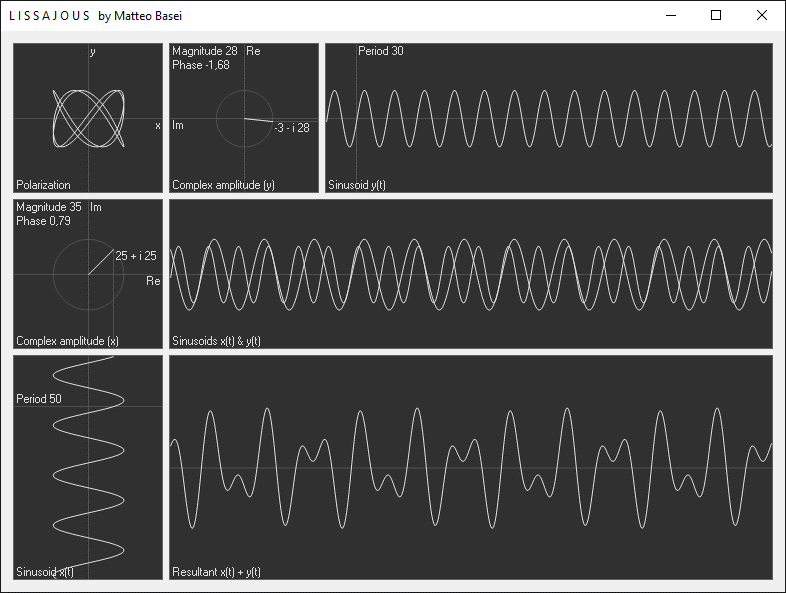
Cambiando la fase di una delle sinusoidi si ottiene una rotazione della figura di Lissajous.

Interferenza e battimenti

Al centro si ha un riquadro cone le due sinusoidi ridisegnate nello stesso grafico, per averne un confronto diretto. Infine in basso si ha il segnale risultante sommando le due sinusoidi. Nel caso in cui le frequenze siano uguali il risultato è banalmente una sinusoide avente medesima frequenza e ampiezza e fase iniziale determinata dalle ampiezze e dallo sfasamento delle due sinusoidi di partenza. Quando le frequenza cambiano è possibile osservare i fenomeni di interferenza. Utilizzando solamente due sinusoidi è già possibile ottenere diverse interessanti forme d'onda, ma sappiamo che incrementando il numero di sinusoidi è possibile realizzare segnali arbitrari (vedi Fourier.exe).

Per determinati valori dei parametri si ha il fenomeno dei battimenti. I battimenti, essendo tanto più accentuati quanto più le frequenze sono vicine, sono molto usate nell'accordatura degli strumenti musicali. La cosiddetta accordatura ad orecchio non è altro che lo sfruttare il fenomeno dei battimenti. Una volta portati i due suoni da accordare a frequenze simili, si ascolta la componente a bassa frequenza generata dai battimenti, e si regola l'intonazione in modo da annullarla per ottenere due suoni perfettamente intonati.

Animazione che mostra il collegamento tra le ampiezze complesse e le sinusoidi. — Animazione che mostra il collegamento tra le ampiezze complesse (in rotazione), le sinusoidi e le figure di Lissajous. In questo caso due sinusoidi con frequenza molto simile generano un battimento molto evidente.