Inertia la lotta contro il moto rettilineo e uniforme
"Immaginate un vasto foglio di carta sul quale Linee rete, Triangoli, Quadrati, Pentagoni, Esagoni e altre figure, invece di restar ferme al loro posto, si muovano liberamente, sulla o nella superficie, ma senza potersene sollevare o sprofondare sotto di essa, molto simili a delle ombre, ma consistenti e dai contorni luminosi."
Inertia è un semplice ed essenziale simulatore spaziale in 2D, uno dei miei più vecchi progetti. Il gioco consiste nel governare la propria navetta manualmente, attivando i propulsori a disposizione e lottando contro l'inerzia. In questo ricorda Asteroids, uno dei videogiochi più famosi di sempre, a cui fa riferimento anche la grafica essenziale in wireframe.

Le prime versioni, risalenti ormai a più di 20 anni fa, le avevo sviluppate in Visual Basic 6. Ultimamente l'ho completamente riscritto in HTML5 e JavaScript (senza utilizzare alcuna libreria) ed è disponibile sotto forma di demo all'indirizzo https://www.matteo-basei.it/inertia-js.
Interfaccia
L'interfaccia è costituita da 5 componenti, lo schermo principale e 4 riquadri, uno per ogni angolo dello schermo. Nello schermo principale sono rappresentati i dati dei "sensori a corto raggio", quindi le navi, le stazioni e i pianeti in scala variabile fino a 1:10 (pixel su metro). È inoltre possibile attivare e disattivare l'anteprima di traiettoria e l'indicazione dei boccaporti di ogni nave o stazione visualizzata.
In alto a destra ci sono i "sensori a lungo raggio", una seconda rappresentazione di navi, stazioni e pianeti in scala variabile da 1:10 a 1:10000. In basso a destra ci sono i "sensori di movimento", dov'è indicata la velocità angolare (in gradi al secondo), la velocità e l'accelerazione (in modulo). Velocità e accelerazione sono anche rappresentati in forma vettoriale.
In basso a sinistra sono presenti i dati dell'oggetto selezionato, tipo, nome del pianeta o classe della nave/stazione, massa, diametro, distanza e direzione. Infine in alto a sinistro è presento lo stato della nave con la massa totale e la quantità di propellente ancora a disposizione.
Spinta, impulso specifico e momento meccanico dei propulsori
Ogni nave è provvista di vari propulsori, ognuno collocato in una specifica posizione e diretto in una specifica direzione. Oltre alla posizione e alla direzione per ogni propulsore è indicata la spinta $F$ (cioè la forza in newton $\text{N}$ ovvero $\text{kg} \, \text{m} \, \text{s}^{-2}$) e l'impulso specifico $I_{sp}$ (in secondi $\text{s}$, vedi Tsiolkovsky per una spiegazione di questa grandezza che in sostanza quantifica l'efficienza del propulsore).
I propulsori si possono prima di tutto dividere in due tipologie: i propulsori principali e quelli di manovra. I propulsori principali sono molto potenti e sono collocati unicamente a poppa, il che costringe, quando vengono utilizzati per raggiungere le alte velocità necessarie per i viaggi interplanetari, ad una manovra di inversione per effettuare la decellerazione necessaria al termine del viaggio.
I propulsori di manovra sono ulteriormente divisi in 6 tipi in base alla loro collocazione e direzione: quelli di poppa, di prua, di sinistra e di dritta e quelli per l'imbardata oraria e antioraria. Questi ultimi agiscono lateralmente per ruotare la nave. Essendo predisposti a coppie la spinta sul baricentro si annulla e va invece calcolato il momento meccanico. Sia $F$ il vettore che rappresenta la spinta del propulsore e $r$ la posizione di tale propulsore rispetto al baricentro della nave, il momento meccanico risulta $$ M_z = r_x F_y - r_y F_x $$ cioè la componente $z$ del prodotto vettoriale $r \times F$. Il momento meccanico ha la dimensione di una forza (la spinta applicata) per una lunghezza (il braccio rispetto al quale è calcolato), quindi ha unità di misura newton per metro ($\text{N} \, \text{m}$ ovvero $\text{kg} \, \text{m}^2 \, \text{s}^{-2}$).
Se per il moto lineare vale l'equazione del moto $F = m \, a$, per il moto rotatorio l'equazione del moto risulta invece $$ M_z = I_z \, \dot \omega_z $$ dove il momento meccanico $M_z$ prende il posto della forza $F$, il momento di inerzia $I_z$ (vedi paragrafo successivo) prende il posto della massa $m$ e l'accelerazione angolare $\dot \omega_z$ ($\omega_z$ indica la velocità angolare) prende il posto dell'accelerazione $a = \dot v$ ($v$ indica la velocità).
Area e momento di inerzia
L'area di un poligono irregolare può essere calcolata grazie alla formula di Gauss che è in sostanza una delle varie declinazioni del teorema di Stokes-Cartan. Siano $\left( x_i , y_i \right)$ gli $n$ vertici del poligono con $i$ che va da $1$ a $n$, ordinati in sequenza, l'area $A$ si calcola $$ A = \frac{1}{2} \left| x_n y_1 - y_n x_1 + \sum_{i = 2}^n \left( x_{i - 1} y_i - y_{i - 1} x_i \right) \right| $$ Facciamo attenzione al fatto che bisogna prendere il modulo della sommatoria in quanto in caso contrario il risultato potrebbe essere positivo o negativo in base al fatto che i vertici siano ordinati in senso orario o antiorario rispetto all'origine del sistema di riferimento (nel nostro caso il baricentro). È altresì importante il fatto che il modulo sia solo sul risultato finale della sommatoria perché i singoli termini saranno positivi o negativi in base all'orientamento dei segmenti e daranno quindi un contributo positivo o negativo all'area finale. La scrittura di questa formula può essere semplificata in $$ A = \frac{1}{2} \left| \sum_{i = 1}^n \left( x_i y_{i + 1} - y_i x_{i + 1} \right) \right| $$ intendendo che $\left( x_{n + 1} , y_{n + 1} \right) = \left( x_1 , y_1 \right)$. O ancora, indicando con $r_i = \left( x_i , y_i \right)$ i vertici del parallelogramma (e intendendo ancora che $r_{n + 1} = r_1$) $$ A = \frac{1}{2} \left| \sum_{i = 1}^n \left( r_i \times r_{i + 1} \right)_z \right| $$ da cui si vede che il fattore $1 / 2$ è coerente con il fatto che il modulo del prodotto vettoriale (nel nostro caso uguale alla componente $z$ essendo le altre due componenti nulle) corrisponde all'area del parallelogramma sottesso dai due vettori.
Il momento di inerzia $I_z$ che compare nell'equazione del moto vista nel paragrafo precedente è calcolato rispetto all'asse $z$ passante per il baricentro dell'oggetto stesso. [...]
Inerzia e gravità
La fisica e la gravità, per quanto in uno spazio bidimensionale, viene simulata in modo realistico, come nel mio programma Newton.exe. È possibile divertirsi ad orbitare intorno a pianeti e ad attraccare a stazioni spaziali o... entrambe le cose: attraccare ad una stazione spaziale orbitante! È possibile attivare o disattivare l'anteprima di traiettoria, che evidenzia se si è in un'orbita circolare, ellittica o in una traiettoria parabolica, e l'anteprima dei boccaporti che aiuta nell'allineamento finale in fase di attracco.
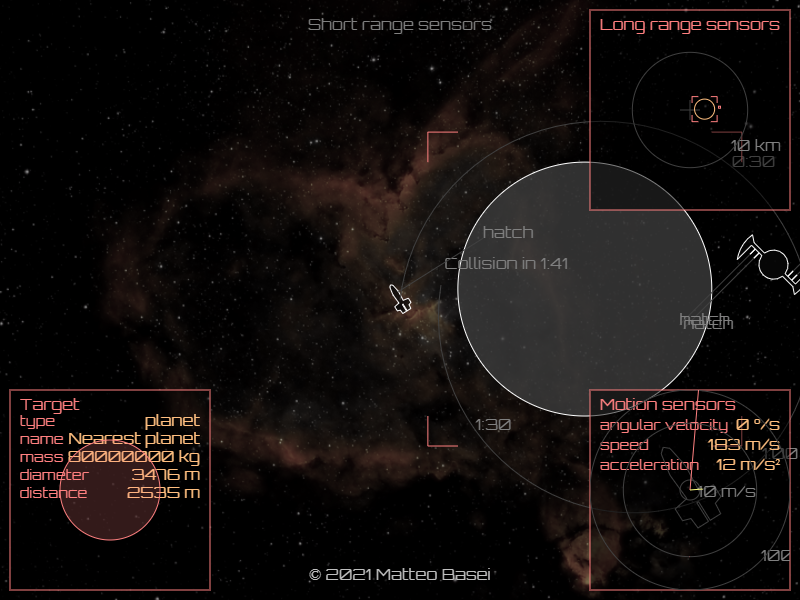
Collisioni
Le collisioni vengono determinate in due passaggi. Prima si considerano le circonferenze aventi come centro il baricentro degli oggetti e come raggio il vertice della sagoma più distante dal baricentro dell'oggetto stesso. Si verifica quindi se la distanza tra i baricentri di due oggetti è inferiore alla somma dei rispettivi raggi e, nel caso due oggetti passino questo primo test, si passa alla verifica dell'intersezione tra i segmenti che compongono le sagome degli oggetti. L'intersezione è calcolata utilizzando la componente z del prodotto vettoriale, che permette di determinare in quale semipiano giace un vertice rispetto ad una retta.
L'algoritmo considera la retta passante per i due vertici di un primo segmento e i due semipiani in cui tale retta divide il piano. Se i due vertici di un secondo segmento giacciono ognuno in un differente semipiano significa che il segmento interseca la retta. Se poi, utilizzando lo stesso metodo, si verifica anche che il primo segmento interseca la retta passante per i due vertici del secondo, allora i due segmenti si intersecano e i due oggetti sono in collisione.
Al momento della collisione i segmenti che costituiscono la sagoma della nave diventano oggetti indipendenti che iniziano a spostarsi e roteare nello spazio, per poi affievolirsi lentamente.
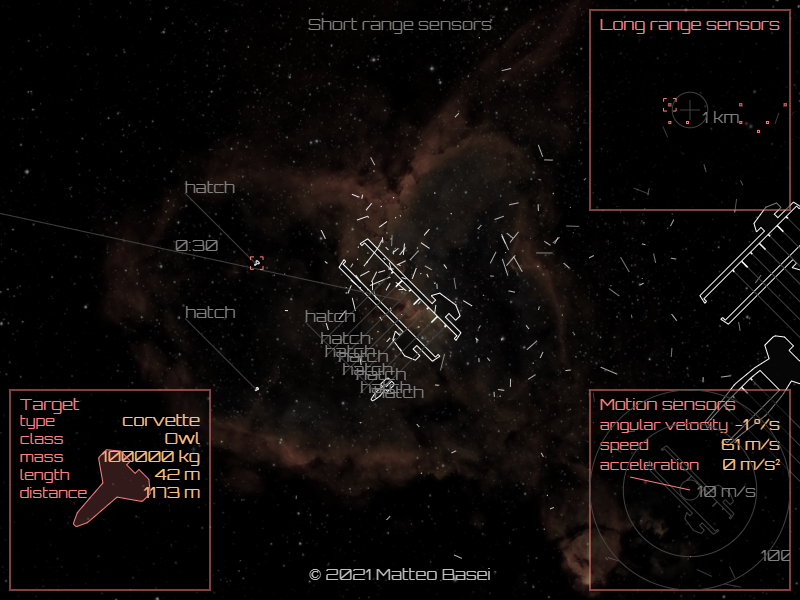
Attracco
Nel caso in cui al momento della collisione tra due oggetti (astronavi o stazioni spaziali) due boccaporti rispettivamente dell'uno e dell'altro oggetto risultino vicini e allineati e le velocità relativa e angolare dei due oggetti siano sotto certe determinate soglie, i due oggetti attraccano l'uno all'altro.

L'eredità di Inertia
Se da una parte Inertia è uno dei miei primi progetti (ho ritrovato alcuni sorgenti datati 2000), dall'altra è la base da cui sono poi partito per lo sviluppo del mio simulatore spaziale 3D Amazing Skies (intorno al 2010).
Lo sviluppo degli algoritmi per la simulazione della fisica e delle collisioni, ad esempio, sono iniziati da qui, in versione bidimensionale. Persino i primi modelli 3D, poi rapidamente rimpiazzati, erano inizialmente le sagome delle navi presenti in questo gioco con l'aggiunta di opportuni vertici e la GUI era inizialmente identica.