ImMap esplorando mondi immaginari

"Non aveva abbastanza immaginazione per poter diventare un matematico."

ImMap è la contrazione di "imaginary map", mappa immaginaria, termini che ho scelto per la loro connotazione evocativa. I matematici, come esploratori e cartografi intenti alla realizzazione delle proprie mappe, esplorano mondi immaginari, pieni di strane forme e idee, annotando ciò che scoprono nella loro cartografia fatta di definizioni e teoremi. Ma $\text{Im}$ è anche il simbolo standard per indicare la parte immaginaria di un numero complesso e il termine mappa in matematica è usato spesso come sinonimo di funzione.

Le funzioni complesse e la loro visualizzazione

Una funzione è una relazione (un sottoinsieme del prodotto cartesiano) tra due insiemi detti dominio e codominio, che associa ad ogni elemento del dominio uno e un solo elemento del condominio. Fintantoché ci si limita a funzioni reali a variabile reale si ha il classico grafico di funzione a cui siamo tutti abituati, facilmente rappresentabile su un foglio o un monitor. Una funzione complessa a variabile complessa è invece un oggetto quadridimensionale (se non ti è familiare la rappresentazione geometrica dei numeri complessi potrebbe interessarti il mio programma Argand.exe).

Per riuscire a rappresentare funzioni come queste restando entro le nostre limitate capacità visive è necessario utilizzare qualche stratagemma. Una possibilità, ad esempio, è l'utilizzo dei colori. Un'altra possibilità, quella seguita in questo programma, è invece quella di impiegare due dimensione per rappresentare il dominio (il classico piano complesso) e con la terza rappresentare una tra la parte reale, la parte immaginaria e il modulo della funzione. Osservando questi tre differenti grafici si riesce a farsi una buona idea di come la funzione dovrebbe effettivamente apparire, a mio parere migliore di quella ottenibile con una rappresentazione che utilizzi i colori.

Questo programma è stato sviluppato in C# e visualizza i grafici in modo volutamente elementare, in bianco e nero e in wireframe, eseguendo tutti i calcoli lato CPU. Il mio focus voleva essere infatti sulle formule e sulla rappresentazione delle funzioni nel modo più semplice, e mi è sembrata consona una grafica austera. In futuro potrei farne una versione con grafica più accattivante, probabilmente in C++ e GLSL, sfruttando le funzionalità delle moderne schede grafiche (ho iniziato a lavorarci, puoi trovare degli aggiornamenti qui ImMap (GLSL)).

Alcune funzioni elementari

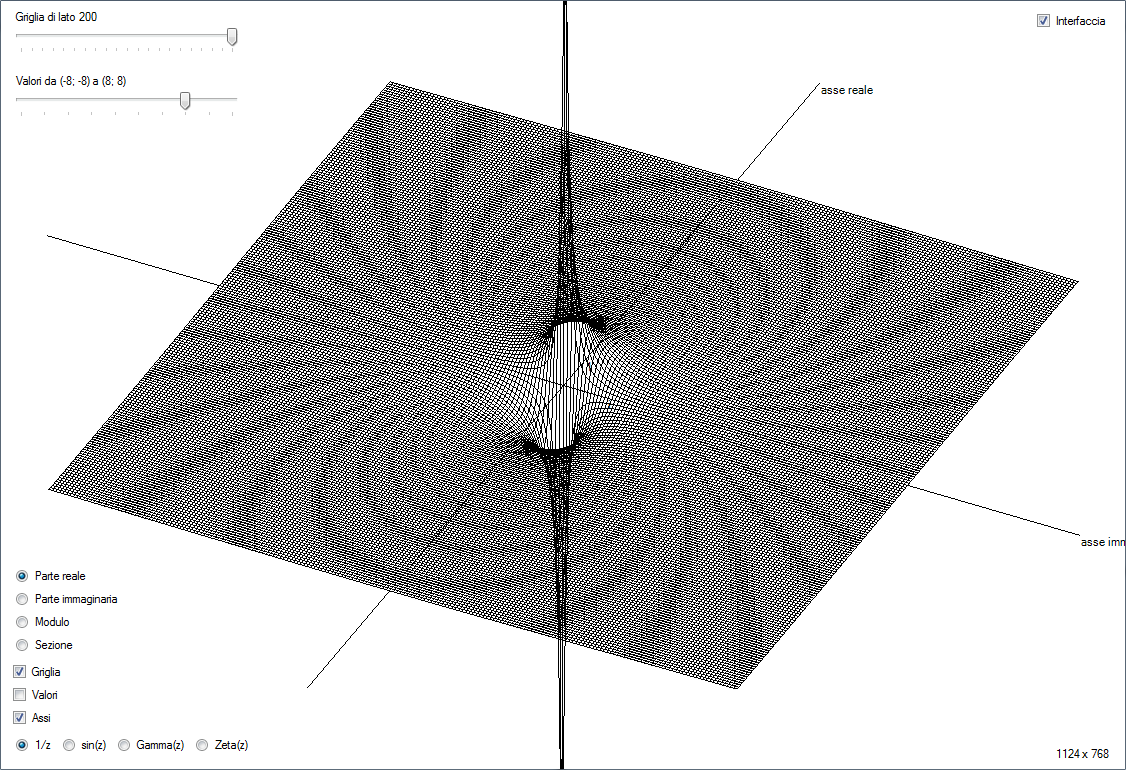
La prima funzione che ho implementato nel mio programma è stata $1 / z$. Questa funzione, che nel campo reale è goffamente spezzata in due, trova la sua forma naturale come funzione complessa.

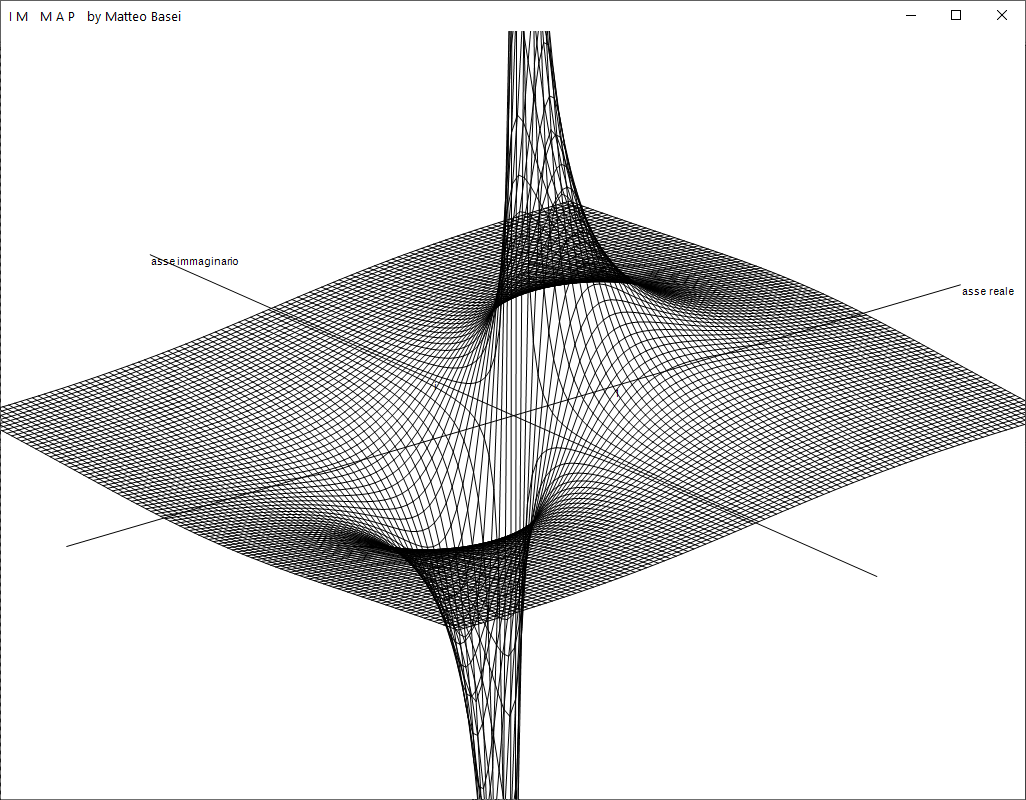
La visualizzazione a griglia con un elevato numero di celle può portare al cosiddetto effetto Moire, che può ricordare un campo magnetico.

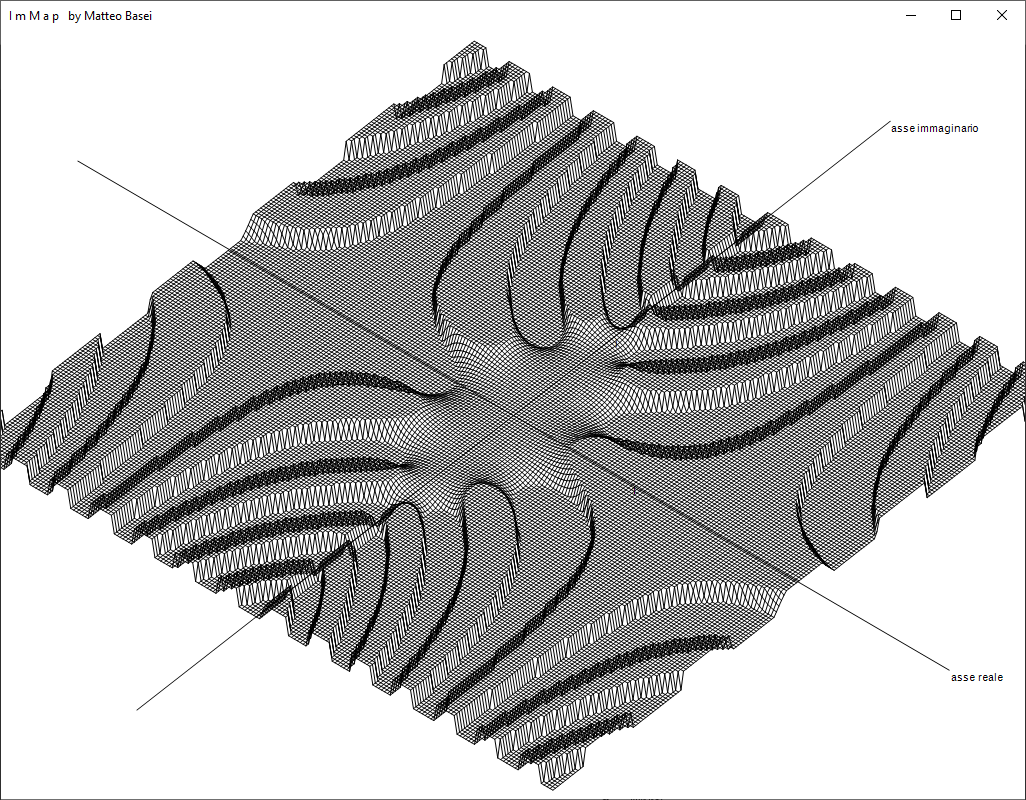
Le sinuose curve della funzione $\sin(z)$.

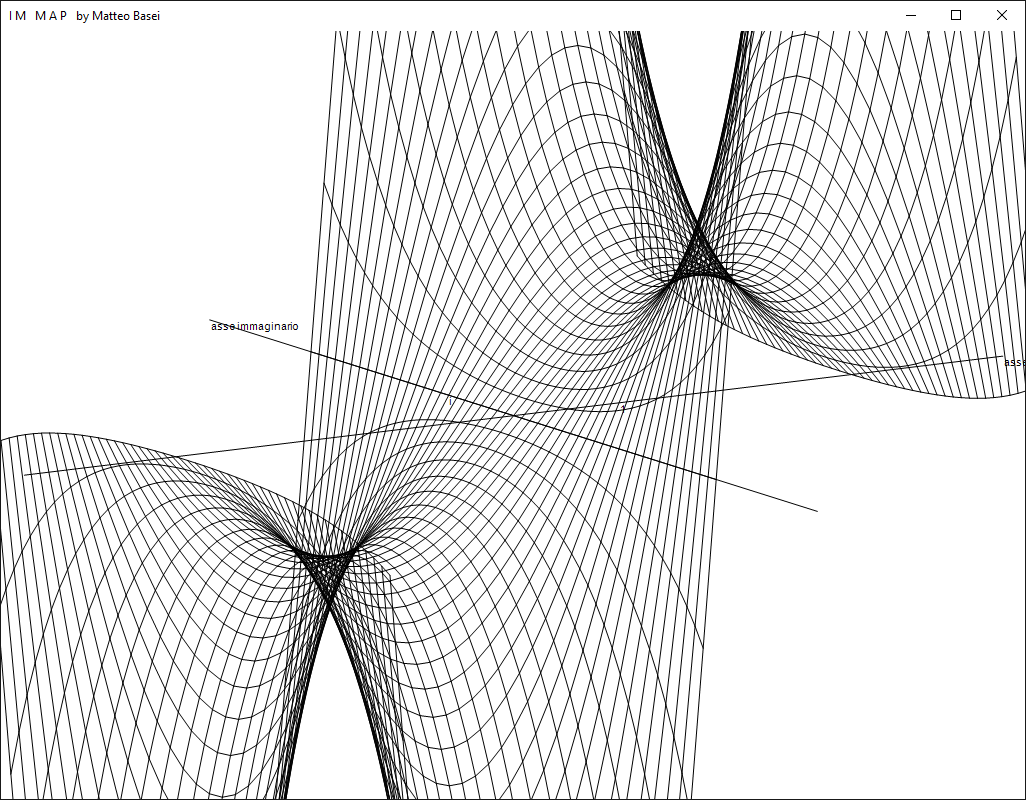
Le funzioni ellittiche

Le funzioni trigonometriche, come la funzione seno vista nella sezione precedente, estese al piano complesso continuano ad essere periodiche solo lungo l'asse reale. Viene naturale chiedersi se esistono funzioni che siano periodiche nel piano complesso in due direzioni. La risposta è sì e le funzioni di questo tipo sono dette funzioni ellittiche, essendo state incontrate per la prima volta in relazioni agli integrali ellittici, a loro volta legati al calcolo della lunghezza di archi di ellissi.

Il metodo più conveniente dal punto di vista del calcolo numerico per definire le funzioni ellittiche è attraverso le funzioni theta di Jacobi. $$ \begin{alignedat}{2} \vartheta_1 \left( z \right) &= 2 \, q^{1/4} \sum_{n = 0}^\infty \left( -1 \right)^n q^{n \left( n + 1 \right)} \sin \Big( \left( 2 \, n + 1 \right) z \Big) \\ \vartheta_2 \left( z \right) &= 2 \,q^{1/4} \sum_{n = 0}^\infty q^{n \left( n + 1 \right)} \cos \Big( \left( 2 \, n + 1 \right) z \Big) \\ \vartheta_3 \left( z \right) &= 1 + 2 \sum_{n = 1}^\infty q^{n^2} \cos \big( 2 \, n \, z \big) \\ \vartheta_4 \left( z \right) &= 1 + 2 \sum_{n = 1}^\infty \left( -1 \right)^n q^{n^2} \cos \big( 2 \, n \, z \big) \end{alignedat} $$ Queste quattro funzione hanno la caratteristica di convergere molto velocemente e quindi per il calcolo numerico la teoria di Jacobi è da preferire rispetto a quella di Weierstrass (che è invece solitamente preferita per uno sviluppo generale della teoria).

La funzione Gamma di Eulero

La funzione Gamma nasce come generalizzazione del fattoriale $n!$ con $n \in \mathbb{N}$ che corrisponde al prodotto degli $n$ interi minori o uguali ad $n$. In particolare, secondo la convenzione introdotta da Legendre, deve essere $$ \Gamma ( n + 1 ) = n! $$ Ci possono essere infinite funzioni reali che interpolando i valori del fattoriale sui numeri interi rispettano questa condizione. Una condizione più stringente è che la funzione per ogni $0 < x \in \mathbb{R}$ rispetti $$ \left\{ \begin{array}{l} f ( 1 ) = 1 \\ f ( x + 1 ) = f ( x ) \, x \end{array} \right. $$ che sono l'equivalente delle proprietà che definiscono ricorsivamente il fattoriale sugli interi $$ \left\{ \begin{array}{l} 0 ! = 1 \\ n ! = \left( n - 1 \right) ! \, n \end{array} \right. $$ Se aggiungiamo la condizione che la funzione sia logaritmicamente convessa, cioè che il logaritmo sia una funzione convessa, per $x > 0$, il teorema di Bohr-Mollerup ci assicura che tale funzione è unica e corrisponde a $$ \Gamma ( x ) = \int_0^\infty {t^{x - 1} e^{-t} dt} $$ dove il secondo membro è chiamato integrale euleriano di secondo tipo.

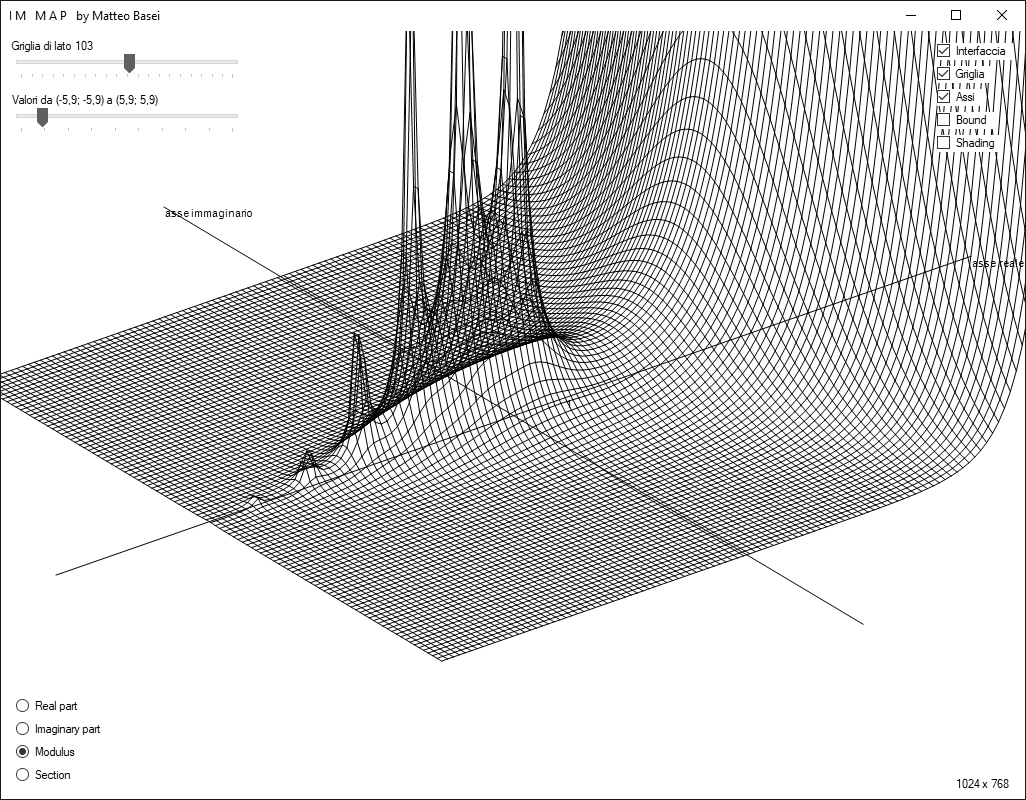
A mio parere una delle più belle immagini che si possono ottenere disegnando funzioni complesse a variabile complessa è la parte reale della funzione Gamma, qui sotto vista "di profilo" (l'asse reale in orizzontale, l'asse immaginario quasi perfettamente perpendicolare allo schermo).

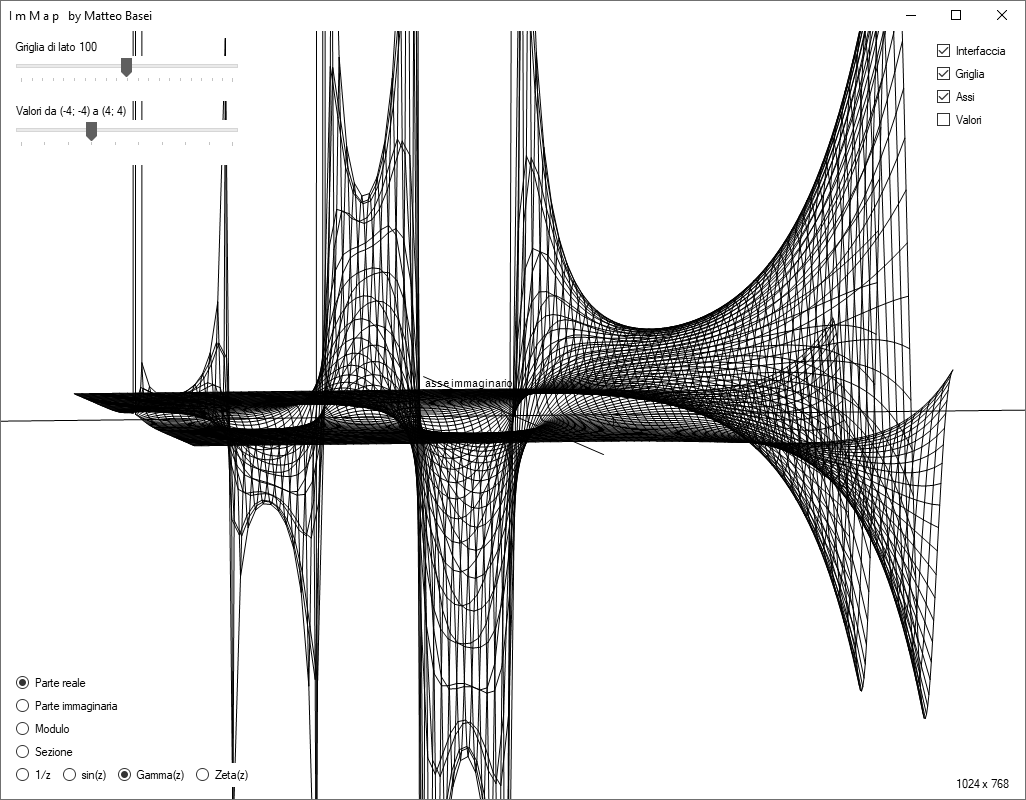
La funzione Gamma viene calcolata utilizzando l'approssimazione Lanczos. Questo metodo è stato sviluppato nel 1964 da Cornelius Lanczos, uno dei cosiddetti "marziani" ungheresi, un gruppo di brillanti scienziati di origini ebraiche emigrati negli Stati Uniti nella prima metà del ventesimo secolo (di cui facevano parte, tra gli altri, scienziati del calibro di Paul Erdos, John von Neumann, Edward Teller e Eugene Wigner).

La funzione Zeta di Riemann

Ed eccoci arrivati alla madre di tutte le funzioni complesse, la funzione Zeta di Riemann, così chiamata in onore di Bernhard Riemann, che per primo la studiò come funzione complessa. L'importanza di questa funzione, come funzione reale, era però già nota a Eulero, che dimostro in modo semplice ed elegante la formula $$ \sum \frac{1}{n^x} = \prod \frac{1}{1 - \frac{1}{p^x}} $$ dove $x$ è un numero reale maggiore di $1$, $n$ prende valori interi positivi e $p$ i valori interi primi.

Per disegnare questa importante funzione ho seguito tre differenti strade. Per valori di $z$ con parte reale strettamente maggiore di $1$ la serie $$ \zeta(z) = \sum \frac{1}{n^z} $$ con $n$ intero positivo è convergente. Per tali valori ho quindi usato semplicemente questa serie troncata ai primi $100$ termini. Per i punti con parte reale minore di $0$ ho invece usato l'equazione funzionale $$ \zeta(z) = 2^z \pi^{z - 1} \sin \left( \frac{\pi z}{2} \right) \Gamma(1 - z) \zeta(1 - z) $$ (dove ricompare la funzione Gamma, che calcolo anche qui con l'approssimazione Lanczos). Infine nella cosiddetta striscia critica (la regione con parte reale compresa tra $0$ e $1$) ho utilizzato il prolungamento analitico che si ottiene attraverso la funzione Eta di Dirichlet, vale a dire $$ \eta(z) = \sum \frac{\left( -1 \right)^{n - 1}}{n^z} $$ Si può dimostrare facilmente che essa è uguale alla funzione Zeta a meno del fattore $1 - 2^{1 - x}$, ma converge per valori con parte reale strettamente positiva. Anche qui ho usato la serie troncata ai primi $100$ termini.

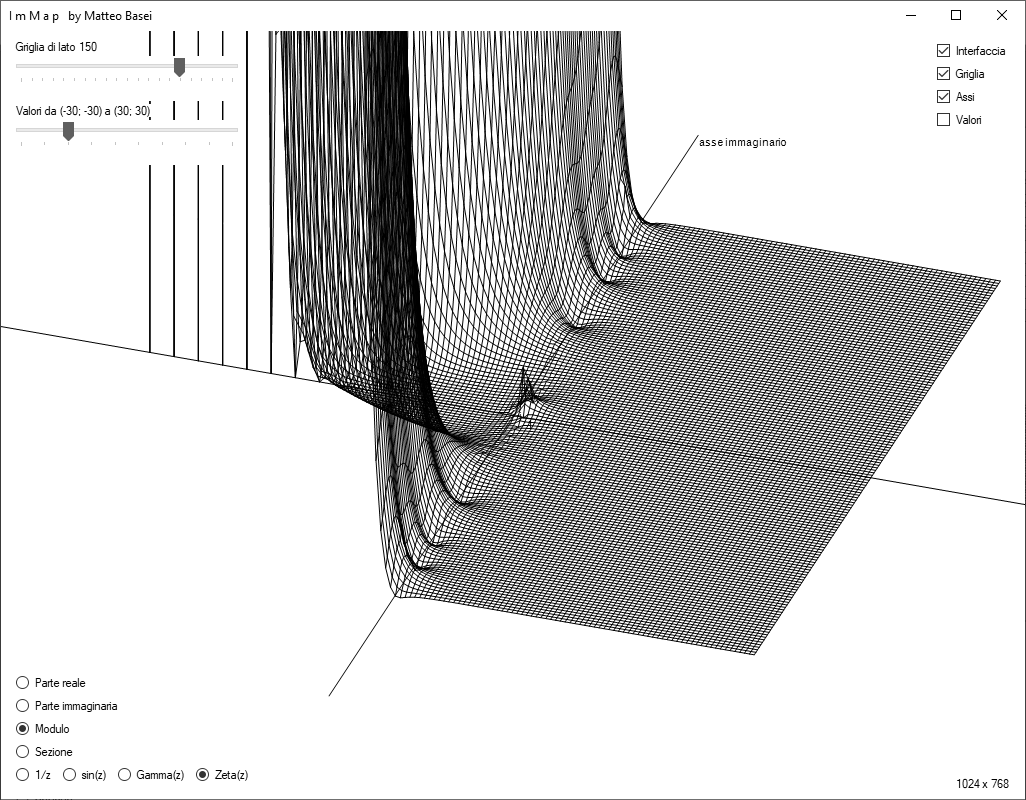
Visualizzandone il modulo si riescono già a vedere chiaramente tutte le caratteristiche salienti della funzione Zeta:

• si vede il polo in $1$, un singolo punto in cui la funzione non è convergente e si comporta in modo simile a come si comporta $1 / z$ intorno all'origine;
• si vedono gli zeri banali, i picchi che scendono in corrispondenza degli interi pari negativi;
• si vedono gli zeri non banali lungo la retta con parte reale pari a $1 / 2$, la cosiddetta retta critica (nell'immagine le prime 3 coppie).

Ma è visualizzandone la parte reale che si riescono ad apprezzare le particolari forme presenti nel semipiano negativo, responsabili degli zeri della funzione (banali e non). Troncando poi i valori nell'intervallo $( −1 , 1 )$ queste forme possono essere visualizzate più chiaramente.

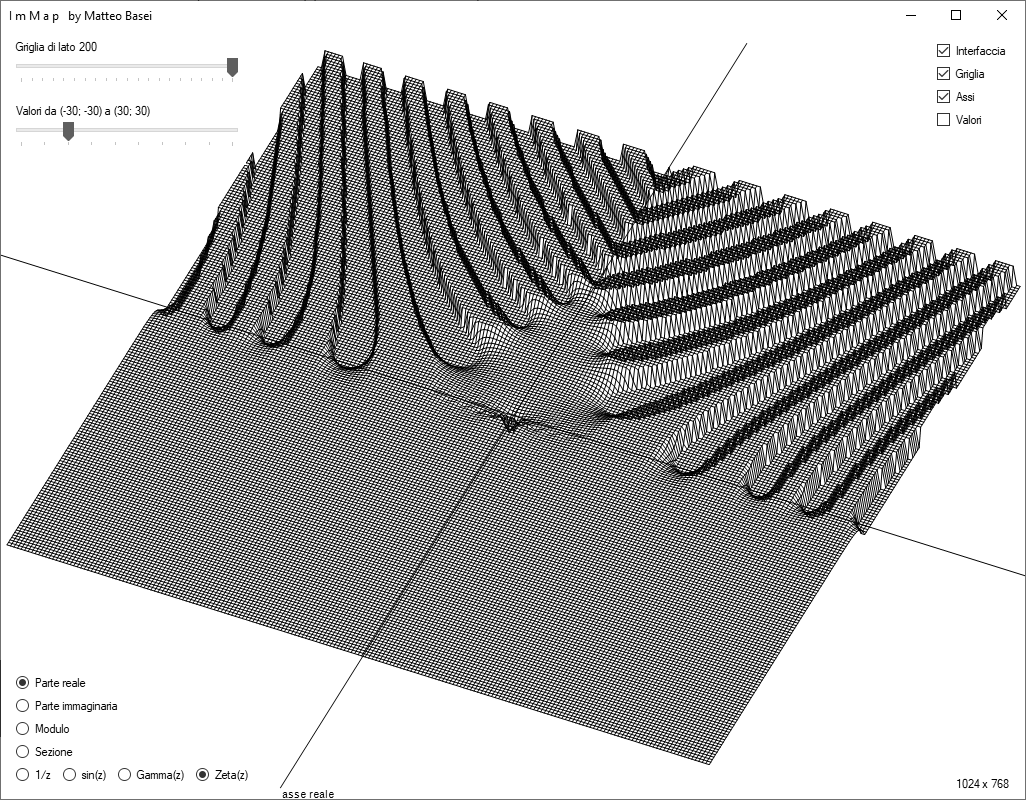
Se ti interessa lo straordinario legame tra gli zeri della funzione Zeta e la distribuzione dei numeri primi potresti dare un'occhiata al mio programma VonMangoldt.exe.