Le clotoidi spirali di spirali di...

Una clotoide (detta anche spirale di Eulero o spirale di Cornu) è una curva la cui curvatura cresce linearmente lungo la propria lunghezza.

Con questo programma ne realizzo una versione discreta, quindi una spezzata, cioè una sequenza di segmenti, ciascuno dei quali forma con il precedente un angolo $\theta$ che aumenta di un certo valore fissato $\Delta \theta$ ad ogni iterazione. Trascurando la lunghezza dei segmenti che la costituiscono (che permettono di regolare lo zoom della figura risultante), ogni possibile spezzata generata è quindi caratterizzata da un unico parametro, la variazione $\Delta \theta$ che viene applicata ad ogni iterazione all'angolo.

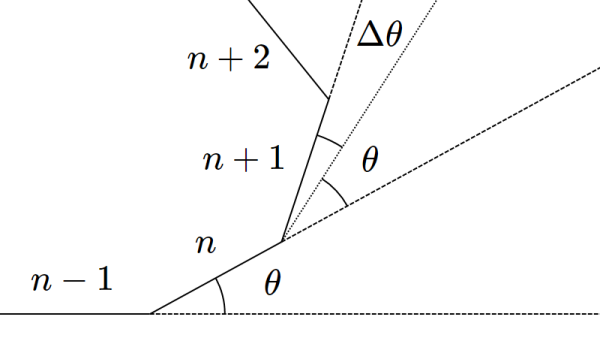
Aumentando costantemente l'angolo $\theta$ si arriverà necessariamente ad un certo punto a superare l'angolo giro. A seconda del valore esatto del parametro $\Delta \theta$, e del rapporto che esso ha con l'angolo giro, si otterrà un nuovo angolo "iniziale" differente e la curva ricomincerà il suo percorso con un certo sfasamento rispetto all'angolo iniziale. In questo modo regolando il parametro è possibile ottenere una gran varietà di differenti figure.

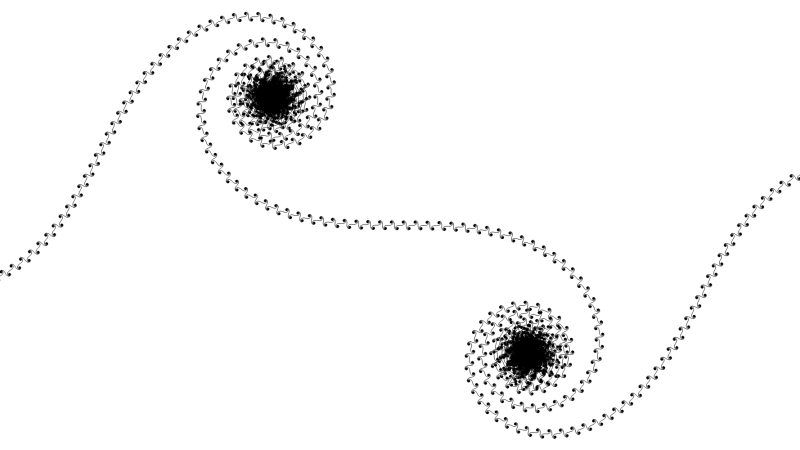
Le clotoidi compaiono nella formulazione degli integrali sui cammini della meccanica quantistica, ed è proprio in questo contesto che le ho incontrate la prima volta, sviluppando la mia simulazione QED.exe, ispirata dal celebre "QED: la strana teoria della luce e della materia" di Richard Feynman.