Bytebeat.exe composizioni in una riga di codice

"La musica è il piacere che la mente umana prova quando conta senza essere conscia di contare."

Questo argomento sembra essere totalmente trascurato, se non da pochissimi appassionati. Inoltre, cosa ancora più strana, in rete non ce n'è traccia prima del 2011. Io ne sono venuto a conoscenza nel 2014 e sono rimasto particolarmente affascinato dalla musica generata dalla formula

(t*9 & t>>4 | t*5 & t>>7 | t*3 & t>>10) - 1

che, nonostante sia relativamente semplice, genera già una melodia tutt'altro che banale.

Il programma che ho sviluppato per esplorare quello che si può fare con la bytebeat (così viene chiamata dai pochi estimatori) oltre a riprodurre il suono mostra il grafico del segnale e permette di salvare il risultato in formato WAV.

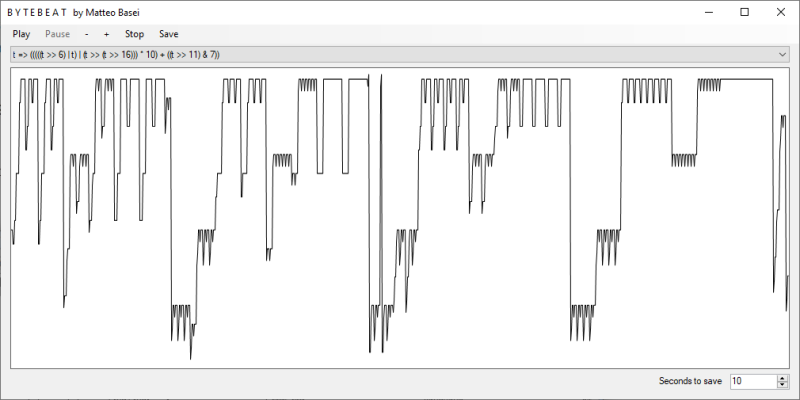
La bytebeat è un tipo particolare di sintesi musicale che utilizza una singola riga di codice. Il codice restituisce la pressione sonora $f(t)$ in funzione del tempo $t$ utilizzando semplici operazione fondamentali. Nelle formule compaiono quindi solamente numeri interi, parentesi, operatori elementari e la variabile $t$.

Campionamento del segnale

La variabile $t$ non è altro che un numero intero che parte da $0$ e che viene incrementato di $1$ ad ogni iterazione del programma. Il segnale musicale generato è campionato a 8 bit e 8000 Hz. Bit è la contrazione di binary digit, quindi significa semplicemente cifra binaria, quindi cifra di un numero in base 2. Campionando a 8 bit avremo quindi che l'ampiezza del nostro segnale potrà assumere 2⁸ = 256 valori, da 0 a 255. Campionare a 8000 Hz significa invece che una sequenza di 8000 valori produrrà un suono della durata di 1 secondo.

Ho trovato in rete alcuni esempi a campionamento maggiore e che utilizzano qualcosa in più delle operazioni fondamentali sugli interi, con conversioni in virgola mobile, utilizzo di funzioni trigonometriche e operatori condizionali ternari. A parer mio questi esempi snaturano il senso stesso della bytebeat, diventando a tutti gli effetti dei classici sintetizzatori. La cosa affascinante della bytebeat è infatti il generare melodie interessanti a partire da formule particolarmente semplici.

I più semplici esempi di bytebeat

Per capire come funziona la bytebeat partiamo dalla più semplice formula che si possa utilizzare per generare musica con questa tecnica, vale a dire semplicemente:

t

In questo caso il valore di uscita corrisponde esattamente al nostro contatore. Essendo però il valore di uscita limitato a 8 bit dopo 2⁸ = 256 iterazioni si otterrà il valore massimo possibile, in binario 11111111. All'iterazione successiva il numero 100000000 in binario verrà troncato, ottenendo 00000000. Il suono prodotto da questa formula sarà quindi un'onda a dente di sega con periodo 256 / 8000 = 0,032 secondi, frequenza 1 / 0,032 = 31,25 Hz, un DO leggermente diminuito. Un suono certamente poco interessante (anche un po' fastidioso per dire la verità).

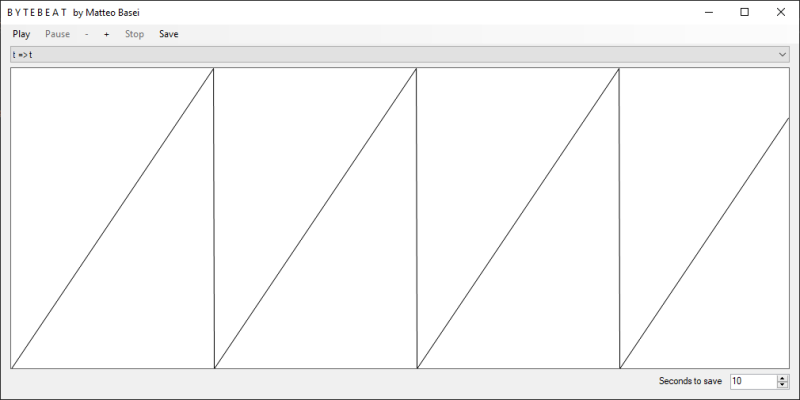
Cosa succede se moltiplichiamo t per una costante? Il suono generato dalla formula

t*5

ad esempio, sarà altrettanto banale, cioè un segnale a dente di sega con periodo 0,032 / 5 = 0,0064 secondi, frequenza 1 / 0,0064 = 156,25 Hz, cioè un MI bemolle 2 ottave sopra al precedente.

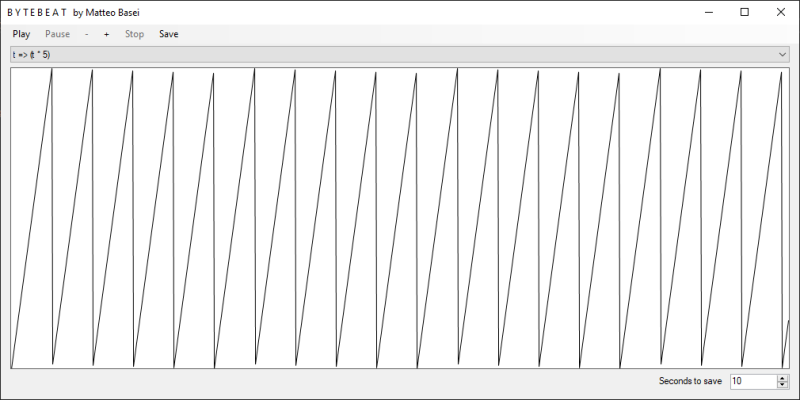
Gli operatori &, | e >>

Prima di continuare una breve nota sugli operatori &, | e >> che compaiono in queste formule, visto che non sono le classiche operazioni numeriche, come somma e moltiplicazione, a cui tutti sono abituati. Gli operatori & e | consistono rispettivamente nella coniugazione e disgiunzione logica dei bit dei due operandi.

>> invece significa che i bit dell'operando a sinistra vengono traslati a destra tante volte quanto indica l'operando di destra. In base 10 questa operazione, che indicheremo con ${>>}_{10}$ per distinguerla da quella in base 2, corrisponde alla divisione per le potenze di 10, ad esempio $$ 314 \, {>>}_{10} \, 1 = 314 / (10^1) = 314 / 10 = 31,4 $$ $$ 314 \, {>>}_{10} \, 2 = 314 / (10^2) = 314 / 100 = 3,14 $$ eccetera. In base 2 corrisponde quindi alla divisione per le potenze di 2. t>>7 corrisponde quindi a t/(2⁷) = t/128. Quindi un'onda a dente di sega di periodo 0,032 * 128 = 4,096 secondi.

Formule composte

Torniamo a noi. La cosa si fa interessante quando si inizia a combinare diverse onde a frequenza differente, in pratica quando nella formula t compare più di una volta. Ad esempio

t*5 & t>>7

produce già una melodia molto interessante e, se notate, è una parte della prima formula citata in questa pagina.

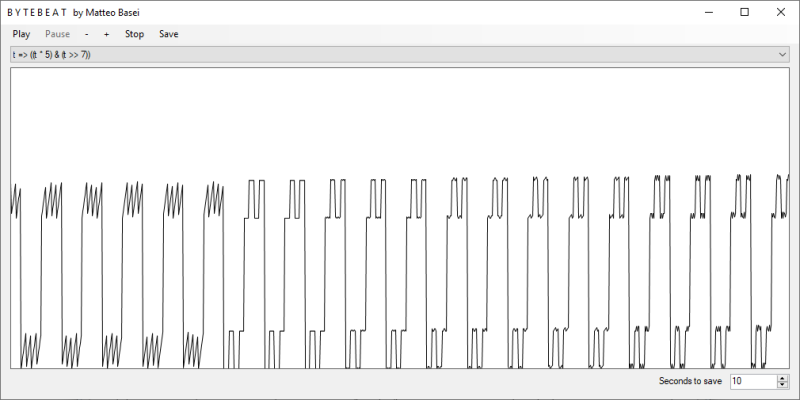
In alcuni casi, più che la melodia e il ritmo generati, risulta interessante la geometria della forma d'onda risultante (vedi ad esempio la prima immagine presente in questa pagina).